Una lógica de secuencias es representada por una serie de condiciones que se suceden unas a otras y que tienen una relación entre sí. Encontrar esta relación ayuda a desarrollar habilidad para comprender las secuencias.
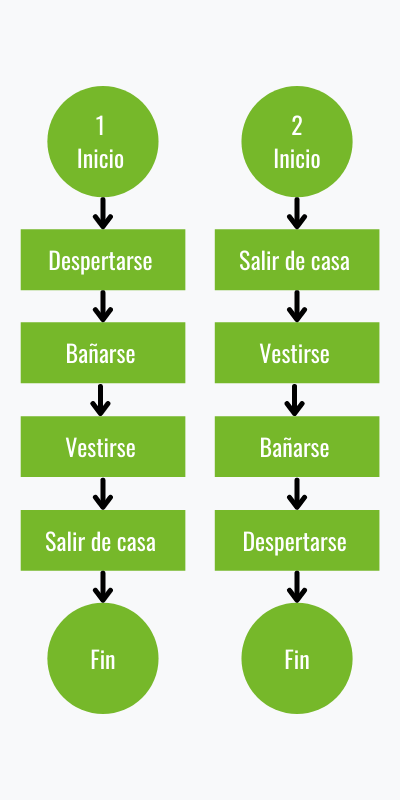
De esta forma, una secuencia es una concatenación de elementos obtenidos a partir de una sucesión. En este ejemplo se observa que la primera secuencia presenta una concatenación de instrucciones que ejecutadas en orden podría decirse que son lógicas. A la izquierda se ha indicado el mismo ejemplo pero en inversa; para el segundo caso el orden de los elementos no permite inferir una secuencia lógica.
Lo bueno de la lógica es que se puede aplicar en escenarios abstractos e incluso reales como las matemáticas, veamos:
1, 3, 5, 7, 11...
En esta secuencia lo primero que se podría observar es que todos los números son impares, pero al ir mas lejos podríamos deducir que el siguiente número es el 13 si se mantiene la lógica de que la secuencia representa los números primos.
9, 16, 23, 30, 37...
Esta otra secuencia combina pares e impares, por lo que se podría concluir que ser par o impar no es una condición de la secuencia. Por otro lado. si se resta el segundo número al primero se obtiene 7. Si se resta el tercer número al segundo se obtiene 7 y lo mismo pasa con los siguientes dos números. Para este caso, una expresión lógica que podría aplicar sería 7*n+2 donde n es un número entero. Para dar continuidad a la secuencia debemos indicar el número correspondiente para la posición número 6; 7*(6)+2=44 por lo que el siguiente número en la secuencia es 44 y se puede aplicar la lógica 7*n+2 para deducir cualquier posición en la secuencia.
Desarrolle la actividad al final de este bloque para obtener 10 puntos en la calificación del curso
